Autocross Italia Driving School.

Tecnica - Cenni di dinamica del veicolo

E purtroppo eccoci arrivati alla teoria. Inevitabile come la pioggia il giorno che vi decidete ad andare in pista a girare. Con qualche conoscenza di base della dinamica del veicolo si arriva sicuramente più lontano, negli sport motoristici, almeno credo. Quindi beccatevi 'sta pappardella e buona lettura! Consiglio comunque di resistere fino alla fine perché io stesso pensandoci e ripensandoci ci ha imparato molte cose che credevo funzionassero in maniera diversa! Per una volta la sQuola è servita a qualcosa. Incredibile. Ringrazio anche alcune letture che ho fatto sulla rete che mi sono servite molto.

LE GOMME

Per capire più a fondo questo tipo di comportamento e necessario trattare il concetto fondamentale della "deriva" della gomma.

LA DERIVA.

Quando entriamo in curva, sterziamo violentemente e sforziamo la gomma, questa reagisce deformandosi elasticamente ed essendo elastica ci restituisce in qualche modo la deformazione che le abbiamo imposto..

Ipotizziamo quindi di essere in rettilineo, a velocità costante e il motore per un attimo non agisce sulle ruote né i freni (condizione di equilibrio).

La ruota (vale sia per anteriore che per posteriore)  vista da davanti appoggia sul terreno ed è deformata poiché deve sopportare il peso del veicolo (o, meglio la parte di esso che le spetta).

Vista dall'alto la ruota si presenterebbe così: l'impronta a terra è definita dall'area tratteggiata che è regolare e simmetrica. Come si vede l'asse dell'impronta coincide con l'asse della ruota. Poiché la ruota gira la parte di gomma che si trova a contatto con l'asfalto (o meglio la spalla del pneumatico) si "schiaccia" e questo succede ad ogni giro della ruota. Questo si chiama "attrito volvente" ed è il responsabile del fatto che più una ruota è sgonfia e più consumiamo benzina e, di riflesso, andiamo meno veloci. Naturalmente se un pneumatico non si deformasse (lo gonfio a 100 bar!) la parte di esso (battistrada) a contatto con l'asfalto e cioè l'impronta a terra, sarebbe piccolissima e questo provocherebbe un bassissimo attrito causando una sicura uscita da pista a ogni curva (è una ipotesi, in realtà esploderebbe prima). Per capire ciò basti pensare alle ruote dei treni che sono piene e di materiale ferroso, con deformazioni veramente minime (ma pur sempre esistenti) e quindi con bassissimo attrito volvente che sono incapaci di dare una qualsiasi direzione alla motrice che non si quella rettilinea, essendo affidata la curva alle  protuberanze laterali delle ruote stesse. Quindi: il pneumatico che si deforma e fa attrito è un bene perché mi da tenuta di strada ma naturalmente entro i limiti del buon senso e quindi rispettando la giusta pressione di gonfiaggio. 

Mettiamo ora di entrare in curva (senza frenare!pazzo!il comportamento in frenata lo vedremo dopo...).

 L'inerzia  è quella forza che impedisce a un qualsiasi corpo di proseguire nel suo stato di quiete o di moto rettilineo uniforme. In sostanza se un corpo procede dritto a una certa velocità, non è facile fargli cambiare idea. Questa forza si manifesta anche in curva ed è chiamata "Forza centrifuga" e più è stretto il raggio della curva e più siamo veloci e più essa e grande (basta pensare ai go-kart). Quindi la forza centrifuga agisce sulla gomma tramite lo chassis e di seguito tramite le sospensioni sulla ruota. Dall'altra parte sulla ruota agisce anche la forza di attrito pneumatico-asfalto. Pertanto alla gomma non resta altro che deformarsi elasticamente come da disegno.

.
Sotto questo sforzo, il punto di contatto con l'asfalto si sposterà verso l'interno della vettura e  l'asse dell'impronta a terra del pneumatico non coincide più con l'asse della ruota:
Primo concetto importante: ANGOLO DI DERIVA (slip angle).

In questo modo si capisce che l'asse della ruota (che rimane sempre quello) e l'asse dell'impronta a terra non coincidono più e si trovano a formare un angolo fra di loro: l'angolo di deriva.

Il problema basilare è semplicemente questo: la gomma non può deformarsi indefinitamente. Fino ad un certo punto, la reazione è lineare, ovvero tanto più io la "carico" (cioè tanto più cerco di sfruttarne l'aderenza), tanto più la gomma, sotto lo sforzo imposto, si deforma e naturalmente più "tiene".

 

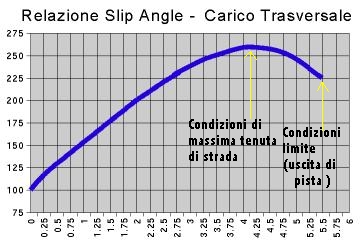
Per capire quello che succede analizziamo il grafico (indicativo per quello che riguarda i valori). Partendo da sinistra in basso sono nelle condizioni suddette di "riposo" e cioè con la ruota che sopporta 100 Kg di peso e con angolo di deriva nullo.

Sterzando, la ruota viene gravata dalla componente della forza centrifuga come spiegato prima e aumenta il suo angolo di scorrimento (stiamo salendo lungo la curva blu). Più sterzo e più vado su nel grafico (anche se la relazione non è perfettamente lineare) fino a quando arriviamo alle condizioni di massima tenuta. Qui si dovrebbe fermare il bravo pilota perché è qui che la gomma mi da il massimo. Purtroppo se insisto oltre questo punto la gomma si deforma sempre più e, quel che è peggio, non è più in grado di sopportare neanche il carico impostole. In sostanza qui inizia il "sottosterzo": insisto a girare il volante ma la vettura non curva. Quello che prima era capace di sopportare (max tenuta) ora non lo è più, ho esagerato. Che fo?

Allargo la traiettoria e ritorno nella condizione di max aderenza.

Insisto col volante fino ad arrivare al punto limite: sono contro le gomme!

Per fortuna le gomme che usiamo nella velocità su terra hanno comportamenti molto intuibili e per così dire "ci avvertono" quando siamo sul punto di andare fuori strada. Differenti quelle delle vetture da turismo e da rally su asfalto , con spalla bassissima e con altissima aderenza ma con un comportamento nervosissimo e difficile da prevedere in condizioni di aderenza limite.

Importante:

Si noti come l'aderenza a questo punto non è niente altro che il frutto di un carico verticale sulla ruota; come dire che più schiaccio il pneumatico e più questo mi dà aderenza. Quindi, in teoria, se non ho sufficiente aderenza (sottosterzo) sarebbe sufficiente aumentare il carico (sterzando di più; facendo la curva più stretta o più veloce) per far aderire meglio il pneumatico! Oppure addirittura se ho una vettura più pesante!

Sembra un controsenso ma in realtà in queste condizioni (tipo vettura che pesa il doppio del mio prototipo tubolare), le condizioni limite del pneumatico (che  non variano se non al variare del pneumatico stesso e tutt'alpiù della geometria delle sospensioni), portano la gomma al limite di aderenza più velocemente e quindi vado fuori prima (sempre contro le gomme!). 

Le vetture da corsa sono leggere il più possibile per questo motivo, riuscendo quindi a "chiedere" al pneumatico meno sforzo per fare le stesse cose di una vettura comune.

DERIVA LONGITUDINALE

Il discorso della deriva, ovviamente, vale nel verso di percorrenza della pista: anche quando accelero e freno la gomma si deforma e ci sarà comunque un limite alla deformazione della gomma che mi consente di andare dritto e non slittare.
Ciò che succede avvicinandosi a questo limite è assolutamente analogo a quello che succede in senso laterale: dapprima comincio a perdere aderenza (fase "calante" della curva) più o meno progressivamente a seconda del tipo di gomma, poi arrivo al limite della deriva e perdo ogni aderenza.

In pratica:

in frenata le ruote si bloccano.

In accelerazione sgommo e la macchina non va avanti.

DERIVA TOTALE

Naturalmente la deriva non e solo longitudinale o trasversale ma può verificarsi contemporaneamente.

Come quando si accelera mentre si curva o quando si frena e si sterza allo stesso tempo.

Esiste un famoso diagramma che consente un po' di capire come la cosa funziona:

Prima di tutto: se le condizioni alle quali viene sottoposta una gomma stanno all'interno dell'area grigia (o dell'ellisse) sono a posto perché non raggiungo il limite di aderenza. 

NOTA. Il fatto che si tratti di ellisse e non di cerchio sottolinea il fatto che le gomme  riescono a dare maggiore aderenza in accelerazione che non in curva.

Secondo concetto importante:

FORZA DI ATTRITO RADENTE.

Il paziente appassionato (paziente perché è arrivato a leggere fin qui) avrà osservato che fin ora ho parlato di attrito con l'asfalto e non con la terra, come avrei dovuto. Questo perché è facilmente intuibile che se la gomma deve arrivare alle condizioni di deriva massima, è necessario che l'attrito con il terreno sia il più grande possibile e non sempre la terra consente tutto ciò. Infatti la terra, ghiaia, sassi, il ghiaccio ecc. hanno un "coefficiente di attrito radente" inferiore a quello dell'asfalto. Ogni superficie ne ha uno e la legge che lo descrive è la seguente:

Forza di attrito = (Ka) * Forza peso 

In pratica, preso una qualsiasi corpo (per esempio un bel cassettone porta libri vecchi della nonna) più pesante è e più difficile è da spostare orizzontalmente (a parità di materiale, nel nostro caso: legno contro pavimento). Il cassettone si muoverà solo se gli applichiamo lateralmente una forza con le nostre braccia e gambe almeno leggermente superiore  alla Forza di attrito. La  Costante è la Ka (coefficiente di attrito). Ogni materiale ha il suo. 

(A voler essere precisissimi una volta mosso il corpo la forza che si deve applicare al corpo può essere anche diversa poiché da attrito statico si passa a quello dinamico, ma qui si va molto per il sottile...).

Come la cassettiera della nonna così si comporta il battistrada del nostro pneumatico nei confronti della terra. Insomma la Ka della terra (che potrebbe valere 0,3 per esempio; per l'asfalto vale 0,55 circa) é inferiore a quella dell'asfalto e quindi non è detto che il pneumatico  riesca a raggiungere l'angolo limite di deriva prima che la gomma "slitti" sulla terra.  

In parole povere ipotizziamo di essere in curva con il mio tubolare e stare sterzando:  i pneumatici esterni sono appena deformati ma sto percorrendo una curva con la terra particolarmente farinosa e non compatta e il peso gravante sulla ruota non è sufficiente per originare una forza di attrito con la terra sufficiente per fare la curva: sono ancora contro le gomme!

Per ovviare a ciò, il prossimo giro passerò su una parte di curva con la terra meno farinosa (Ka superiore, maggiore aderenza) o farò la curva più lentamente, oppure giocherò con acceleratore e freno in modo tale da far spostare il peso sulle ruote quel tanto che basta per aumentare l'aderenza aumentando per un attimo il carico e consentire di compiere la curva; in questo caso però sta molto alla sensibilità del pilota riuscire ad arrivare al" limite" senza superarlo.

Un altro classico caso è quando si è in frenata; se si prova a far curvare il retrotreno questo è così alleggerito che immediatamente parte a sbandare perché non ha sufficiente aderenza (c'è poco peso sul retrotreno mentre le sospensioni anteriori sono a "fondo corsa"). Allora basta allentare il freno per ridurre il trasferimento di carico verso l'avantreno che alleggeriva ne contempo il retrotreno, il peso "ritorna" sul retrotreno che può quindi ritrovare l'aderenza.

Ma se la gomma stava slittando perché si era raggiunto l'angolo limite di deriva, sarà inutile trasferire più carico, perché peggiorerà solo le cose. Per definizione, infatti, l'angolo limite di deriva è il limite di carico sopportabile dalla gomma senza slittare, superato questo angolo non esiste alcun carico verticale in grado di far riprendere aderenza alla gomma!

NOTA. Secondo questa regola l'aderenza dovuta alla forza di attrito NON DIPENDE dalla porzione di gomma che si deforma! Per questo anche il ciclista da corsa con i suoi "Palmer" superstretti riesce tranquillamente a curvare anche a grandi velocità. Naturalmente se è un po' sovrappeso la gomma si deforma presto e addio ciclista! Inoltre attenzione alla sabbiolina sul bordo della strada fa calare repentinamente il coefficiente di aderenza e...allacciare il casco! Naturalmente il vantaggio è che si ha meno attrito volvente e quindi si fa meno fatica, almeno in pianura.

Finalmente abbiamo capito perché le vetture delle gare sul ghiaccio hanno pneumatici molto stretti, come quelli della Panda. Si tratta in questo caso di un terreno particolarmente viscido e con scarsissima aderenza. Quindi in pneumatico difficilmente in accelerazione,frenata e curva riuscirà mai ad arrivare al limite di deriva in quanto la sua deformazione è minima. Allora è più conveniente tentare di aumentare il carico (cioè il peso) sul pneumatico che, come abbiamo capito, moltiplicato per una costante dà la forza di attrito e cioè l'aderenza. Quindi, a parità di peso sul pneumatico stesso, se la superficie è minore, si ha una pressione per unità di superficie maggiore e questo mi porta una migliore aderenza a parità di condizioni. Se facessimo lo stesso discorso se fossimo sull'asfalto avremmo , è vero, maggior forza di attrito ma contemporaneamente il pneumatico troppo stretto si deformerebbe fino al limite di deriva a ogni minima sollecitazione e saremmo subito fuori pista o in testacoda! Se poi vogliamo inserire dei chiodi all'interno del battistrada il pneumatico riesce a "entrare" nel ghiaccio meglio e la vettura pattina di meno.

Quindi: se si vuole avere una vettura che "tiene" in curva e che non slitti in accelerazione e in frenata su di essa vanno montate gomme più larghe possibile. In questo modo l'impronta a terra aumenta, con conseguente aumento della tenuta. Tutto ciò, però, provoca naturalmente un aumento delle perdite per attrito al rotolamento. Ma qual'è la misura giusta? Nel nostro sport preferito va prima di tutto considerato che ci sono delle misure limite  date dai regolamenti ufficiali . Inoltre  va considerato il fatto che in caso di scarsa aderenza si può giungere al limite di aderenza per attrito senza mai raggiungere il limite di deriva. In questi casi sarebbe inutile utilizzare pneumatici esageratamente larghi, che favoriscono l'allontanamento del limite di deriva, tanto quel punto non verrà mai raggiunto. Viene allora utilizzata una larghezza che è quella giusta per sfruttare il pneumatici al massimo delle loro possibilità. Per questo sono indispensabili le prove in circuito e le sensazioni del pilota.

Conclusioni:

Il pneumatico segue essenzialmente due regole:

Angolo di Deriva. L'aderenza è proporzionale (non linearmente) alla deformazione del battistrada. Più premo sulla gomma in curva è più ho aderenza (ma non linearmente). Questo però fino a un limite che è proprio del pneumatico. Di qui in poi si va fuori strada.

Forza di attrito. Proporzionale al carico in modo lineare. Si ottiene moltiplicando il carico Più premo e più ho aderenza.

Posso però uscire di pista per entrambi questi fenomeni, per esempio:

Caricando troppo il pneumatico sull'asfalto lo deformo troppo ed esco di pista (deriva). Caricando il pneumatico sulla terra che, essendo sdrucciolevole, non ce la fa a "tenere" ed esco di pista (attrito).

Altre nozioni sulla frenata e il comportamento in curva: Driving: dinamica del veicolo seconda parte